Chapter 8 The Disjoint Set Class

8.1 Equivalence Relations

A relation is defined on a set if for every pair of elements , is either true or false. If is true, then we say that is related to .

An equivalence relation is a relation that satisfies three properties:

1. (Reflexive) , for all .
2. (Symmetric) if and only if .
3. (Transitive) and implies that .

8.2 The Dynamic Equivalence Problem

Given an equivalence relation , the natural problem is to decide, for any and , if .

The equivalence class of an element is the subset of that contains all the elements that are related to . To decide if , we need only to check whether and are in the same equivalence class.

The input is initially a collection of sets, each with one element. This initial representation is that all relations (except reflexive relations) are false. Each set has a different element, so that ; this makes the sets disjoint.

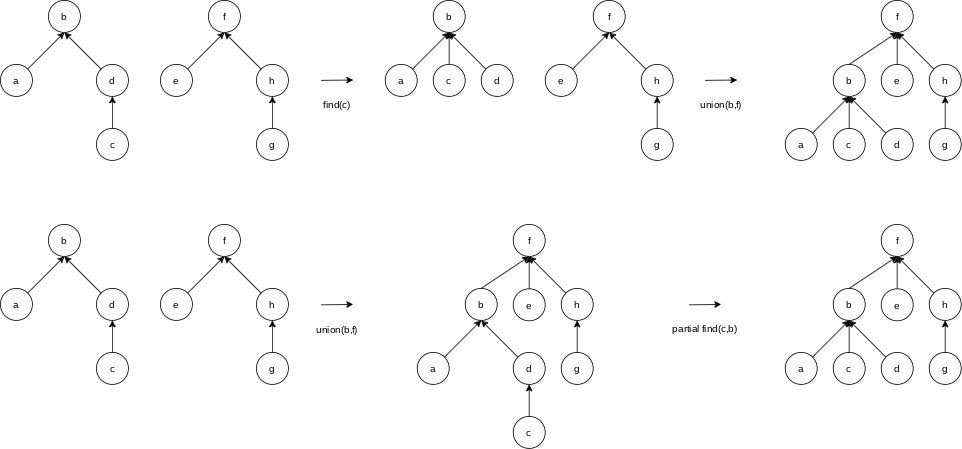
There are two permissible operations. The first is find, which returns the name of the set (that is, the equivalence class) containing a given element. The second operation adds relations. If we want to add the relation , then we first see if and are already related. This is done by performing finds on both and and checking whether they are in the same equivalence class. If they are not, then we apply union. This operation merges the two equivalence classes containing and into a new equivalence class. From a set point of view, the result of is to create a new set , destroying the originals and preserving the disjointness of all the sets. The algorithm to do this is frequently known as the disjoint set union/find algorithm for this reason.

This algorithm is dynamic because, during the course of the algorithm, the sets can change via the union operation. The algorithm must also operate online: When a find is performed, it must give an answer before continuing. Another possibility would be an off-line algorithm.

Notice that we do not perform any operations comparing the relative values of elements but merely require knowledge of their location. For this reason, we can assume that all the elements have been numbered sequentially from to and that the numbering can be determined easily by some hashing scheme. Thus, initially we have for through .

Our second observation is that the name of the set returned by find is actually fairly arbitrary. All that really matters is that find(a) == find(b) is true if and only if and are in the same set.

There are two strategies to solve this problem. One ensures that the find instruction can be executed in constant worst-case time, and the other ensures that the union instruction can be executed in constant worst-case time. It has been shown that both cannot be done simultaneously in constant worst-case time.

We will now briefly discuss the first approach. For the find operation to be fast, we could maintain, in an array, the name of the equivalence class for each element. Then find is just a simple lookup. Suppose we want to perform union(a, b). Suppose that is in equivalence class and is in equivalence class . Then we scan down the array, changing all ’s to . Unfortunately, this scan takes . Thus, a sequence of unions (the maximum, since then everything is in one set) would take time. If there are find operations, this performance is fine, since the total running time would then amount to for each union or find operation over the course of the algorithm. If there are fewer finds, this bound is not acceptable.

One idea is to keep all the elements that are in the same equivalence class in a linked list. This saves time when updating, because we do not have to search through the entire array. This by itself does not reduce the asymptotic running time, because it is still possible to perform equivalence class updates over the course of the algorithm.

If we also keep track of the size of each equivalence class, and when performing unions we change the name of the smaller equivalence class to the larger, then the total time spent for merges is . The reason for this is that each element can have its equivalence class changed at most times, since every time its class is changed, its new equivalence class is at least twice as large as its old. Using this strategy, any sequence of finds and up to unions takes at most time.

8.3 Basic Data Structure

Using the strategy above, it is possible to create a tree of depth , so the worst-case running time of a find is . Typically, the running time is computed for a sequence of intermixed instructions. In this case, consecutive operations could take time in the worst case.

8.4 Smart Union Algorithms

The unions above were performed rather arbitrarily, by making the second tree a subtree of the first. A simple improvement is always to make the smaller tree a subtree of the larger, breaking ties by any method; we call this approach union-by-size.

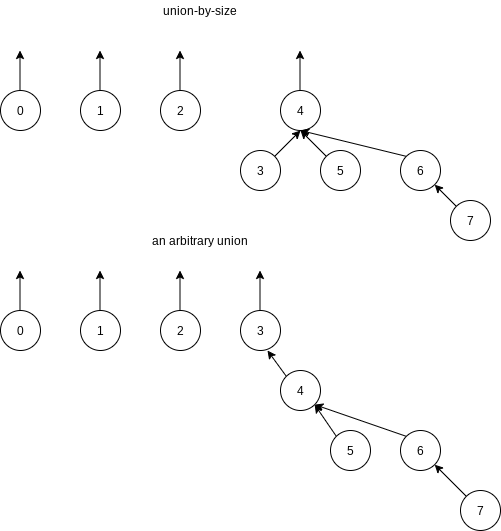
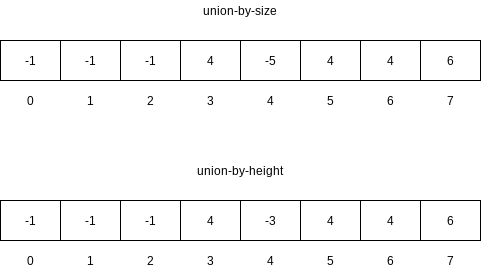
To implement this strategy, we need to keep track of the size of each tree. Since we are really just using an array, we can have the array entry of each root contain the negative of the size of its tree. Thus, initially the array representation of the tree is all ’s. When a union is performed, check the sizes; the new size is the sum of the old. Thus, union-by-size is not at all difficult to implement and requires no extra space. It is also fast, on average.

An alternative implementation, which also guarantees that all the trees will have depth at most , is union-by-height. We keep track of the height, instead of the size, of each tree and perform unions by making the shallow tree a subtree of the deeper tree.

8.5 Path Compression

Path compression is performed during a find operation and is independent of the strategy used to perform unions. Suppose the operation is . Then the effect of path compression is that every node on the path from to the root has its parent changed to the root.

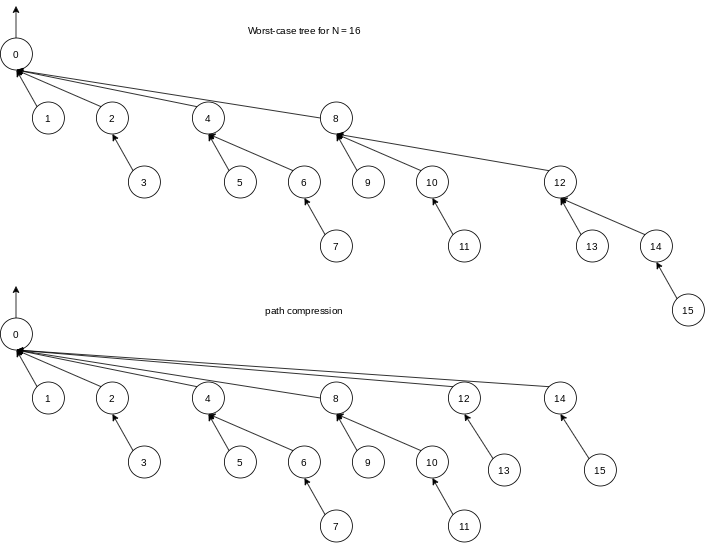
Path compression is perfectly compatible with union-by-size, and thus both routines can be implemented at the same time.

Path compression is not entirely compatible with union-by-height, because path compression can change the heights of the trees. It is not at all clear how to recompute them efficiently. The answer is do not!! Then the heights stored for each tree become estimated heights (sometimes known as ranks), but it turns out that union-by-rank (which is what this has now become) is just as efficient in theory as union-by-size.

8.6 Worst Case for Union-by-Rank and Path Compression

When both heuristics are used, the algorithm is almost linear in the worst case. Specifically, the time required in the worst case is (provided ), where is an incredibly slowly growing function that for all intents and purposes is at most for any problem instance. However, is not a constant, so the running time is not linear.

8.6.1 Slowly Growing Functions

Consider the recurrence:

In this equation, represents the number of times, starting at , that we must iteratively apply until we reach (or less). We assume that is a nicely defined function that reduces . Call the solution to the equation .

There are the solution for , for various . In our case, we are most interested in . The solution is known as the iterated logarithm.

8.6.2 An Analysis By Recursive Decomposition

---

Lemma 8.1.

When executing a sequence of union instructions, a node of rank must have at least one child of rank .

Proof.

By induction. The basis is clearly true. When a node grows from rank to rank , it obtains a child of rank . By the inductive hypothesis, it already has children of ranks , thus establishing the lemma.

---

---

Lemma 8.2.

At any point in the union/find algorithm, the ranks of the nodes on a path from the leaf to a root increase monotonically.

Proof.

The lemma is obvious if there is no path compression. If, after path compression, some node is a descendant of , then clearly must have been a descendant of when only unions were considered. Hence the rank of is less than the rank of .

---

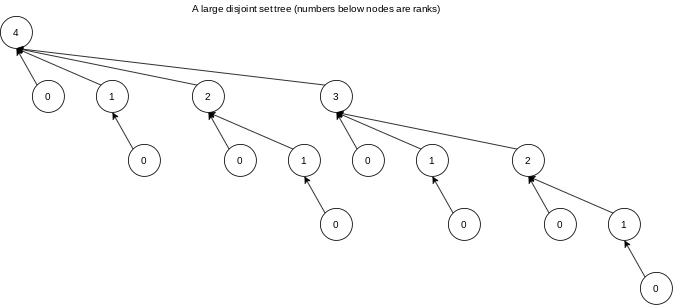
Partial Path Compression

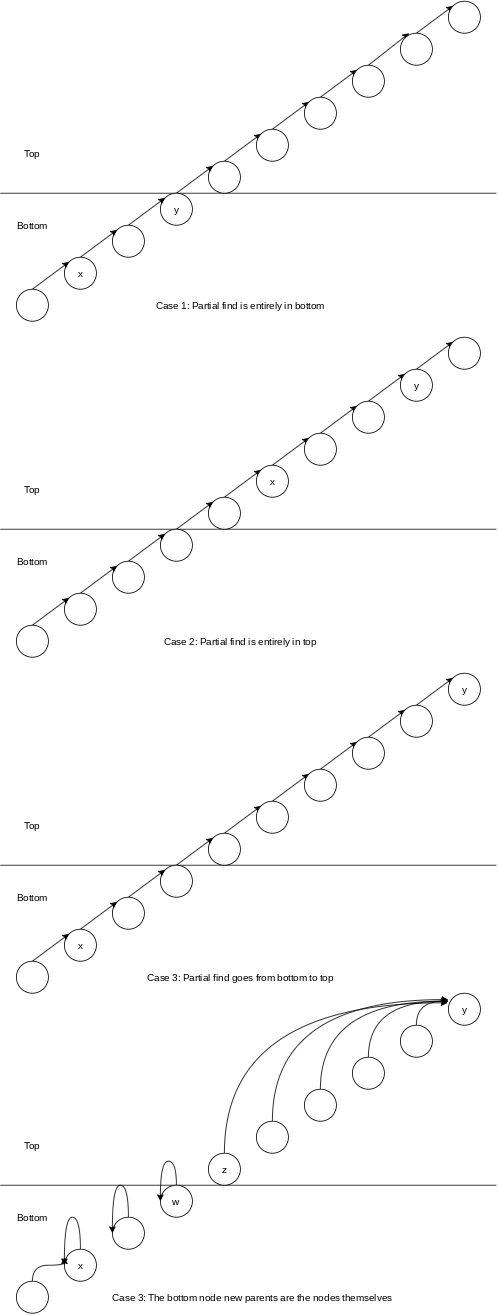
A partial find operation specifies the search item and the node up to which the path compression is performed.

A Recursive Decomposition

What we would like to do next is to divide each tree into two halves: a top half and a bottom half. We would then like to ensure that the number of partial find operations in the top half plus the number of partial find operations in the bottom half is exactly the same as the total number of partial find operations. We would then like to write a formula for the total path compression cost in the tree in terms of the path compression cost in the top half plus the path compression cost in the bottom half.

Let be the total number of original partial find operations. Let be the total number of nodes. Let be the total number of non-root bottom nodes.

---

Lemma 8.3.

.

Proof.

In cases and , each original partial find operation is replaced by a partial find on the top half, and in case , it is replaced by a partial find on the bottom half. Thus each partial find is replaced by exactly one partial find operation on one of the halves.

---

---

Lemma 8.4.

Let be the number of parent changes for a sequence of finds with path compression on items, whose maximum rank is . Suppose we partition so that all nodes with rank at or lower are in the bottom, and the remaining nodes are in the top. Assuming appropriate initial conditions,

Proof.

The path compression that is performed in each of the three cases is covered by . Node in case is accounted for by . Finally, all the other bottom nodes on the path are non-root nodes that can have their parent set to themselves at most once in the entire sequence of compressions. They are accounted for by .

---

If union-by-rank is used, then by Lemma , every top node has children of ranks prior to the commencement of the partial find operations. Each of those children are definitely root nodes in the bottom (their parent is a top node). So for each top node, nodes (the children plus the top node itself) are definitely not included in .

---

Lemma 8.5.

Let be the number of parent changes for a sequence of finds with path compression on items, whose maximum rank is . Suppose we partition so that all nodes with rank at or lower are in the bottom, and the remaining nodes are in the top. Assuming appropriate initial conditions,

Proof.

Substitute into Lemma 8.4.

---

---

Theorem 8.1.

.

Proof.

We start with Lemmas :

Observe that in the top half, there are only nodes of rank , and thus no node can have its parent change more than times. This yields a trivial bound of for . Thus,

Combining terms,

Select . Then , so

Equivalently, since according to Lemma , (the proof falls apart without this),

Let ; then

which implies . This yields .

---

---

Theorem 8.2.

Any sequence of unions and finds with path compression makes at most parent changes during the finds.

Proof.

The bound is immediate from Theorem since .

---

8.6.3 An O(M log* N) Bound

---

Theorem 8.3.

.

Proof.

From Lemma we have,

and by Theorem , . Thus,

Rearranging and combining terms yields

So choose . Clearly, this choice implies that , and thus we obtain

Rearranging as in Theorem , we obtain,

This time, let ; then

which implies . This yields .

---

8.6.4 An O(Ma(M,N)) Bound

---

Theorem 8.4.

.

Proof.

Following the steps in the proof of Theorem .

Needless to say, we could continue this ad-infinitim. Thus with a bit of math, we get a progression of bounds:

$$
\begin{align}
C(M, N, r) &< 2M + N \log^{}r \
C(M, N, r) &< 3M + N \log^{}r \
C(M, N, r) &< 4M + N \log^{}r \
C(M, N, r) &< 5M + N \log^{****}r \
C(M, N, r) &< 6M + N \log^{*****} r
\end{align}
$$

Each of these bounds would seem to be better than the previous since, after all, the more $\log{\dots}r\log^{\dots}r\log^{***}r6M5M$ term.

Thus what we would like to do is to optimize the number of s that are used.

Define to represent the optimal number of s that will be used. Specifically,

Then, the running time of the union/find algorithm can be bounded by .

---

---

Theorem 8.5.

Any sequence of unions and finds with path compression makes at most

parent changes during the finds.

Proof.

This follows from the above discussion, and the fact that .

---

---

Theorem 8.6.

Any sequence of unions and finds with path compression makes at most parent changes during the finds.

Proof.

In Theorem , choose to be ; thus we obtain a bound of , or .

---

8.7 An Application

A simple algorithm to generate the maze is to start with walls everywhere (except for the entrance and exit). We then continually choose a wall randomly, and knock it down if the cells that the wall separates are not already connected to each other. If we repeat this process until the starting and ending cells are connected, then we have a maze.